Parte 1: Le equazioni di Maxwell
(questo post è apparso su sito del disf, Documentazione Interdisciplinare di Scienza e Fede nell'ambito su una serie di articoli su "La luce e la filosofia della scienza", per l'anno internazionale della luce)
Pur essendo la luce uno dei mezzi principali con cui percepiamo ed investighiamo il mondo che ci circonda, una comprensione della sua reale natura e dei fenomeni ad essa connessi è stata possibile solo con i progressi compiuti tra il XIX e XX secolo.
Figura 1. Il campo magnetico generato da una calamita. Il carattere dipolare delle linee di forza è evidenziato dalla limatura di ferro che è attratta da esso.
Un primo grande passo fu la descrizione unificata di elettricità e magnetismo, noti – ma considerati distinti – da migliaia di anni: sfregando due panni di tessuti diversi questi si caricano di cariche elettriche uguali ed opposte che generano un campo elettrico. Analogamente una calamita genera un campo magnetico[1], con poli diversi che si attraggono e uguali che si respingono (Figura 1).
Realizzando i primi circuiti elettrici si notò che un filo percorso da corrente, quindi da cariche elettriche in movimento, genera un campo magnetico (Oersted, 1820); analogamente un campo magnetico deflette la traiettoria di una carica elettrica (Forza di Lorentz, ma derivata per primo da Oliver Heaviside nel 1889).
Questi indizi mostrarono come ci dovesse essere una relazione tra cariche elettriche e campi magnetici. Si trattava comunque di casi stazionari, e quindi non dipendenti dal tempo, che non consentivano di apprezzare l'intima connessione tra i due fenomeni, investigata inizialmente da Faraday. Nel 1831, infatti, Faraday osservò che, ponendo un circuito elettrico in un campo magnetico e aumentando o diminuendo l’intensità del campo, si generava nel circuito una corrente elettrica: la variazione di campo magnetico generava un campo elettrico che faceva muoveva le cariche nel circuito.
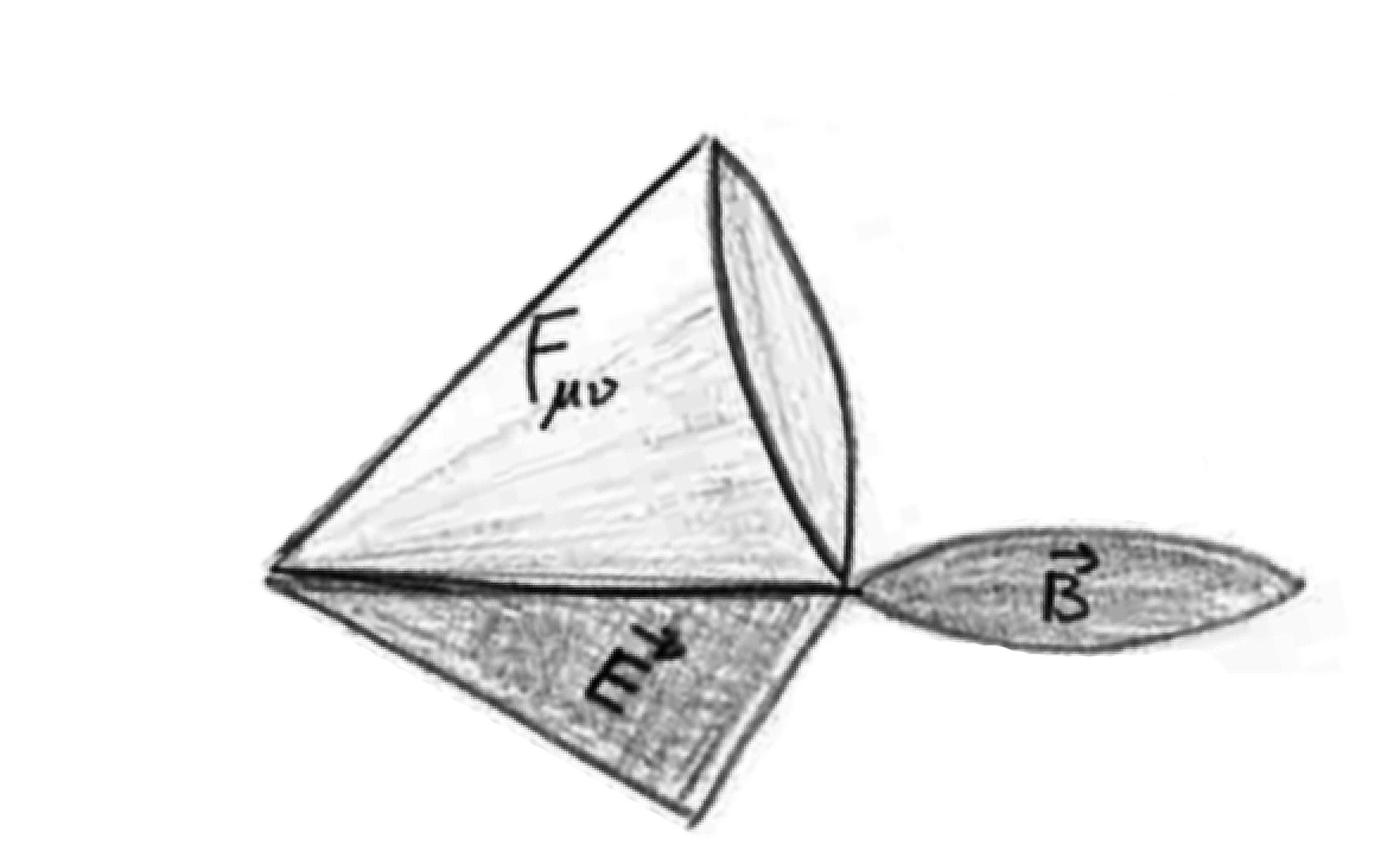
Figura 2. Il campo elettromagnetico (matrice Fμν) è rappresentato, in questo caso, da un cono a base circolare. Le sue "ombre" possono apparirci molto diverse a seconda della prospettiva Nel caso 1. come un triangolo (campo elettrico) mentre nel caso 2. come un'ellisse (campo magnetico), ma sono solo aspetti differenti dello stesso fenomeno.
Successivamente Maxwell notò come variazioni di campo elettrico generavano un campo magnetico e riportò i suoi risultati in un lavoro del 1861, On physical lines of force. In questo fondamentale articolo sono presenti le quattro equazioni del campo elettromagnetico che poi prenderanno il suo nome. Esse racchiudono tutte le proprietà dei fenomeni elettrici e magnetici e ne forniscono una trattazione valida ancora oggi.
L'unificazione dei campi elettrici e magnetici in una sola teoria fu un enorme balzo in avanti concettuale. Tramite le equazioni di Maxwell è stato possibile progredire da una visione di ombre bidimensionali, rappresentate dai distinti campi elettrici e magnetici, alla comprensione del reale oggetto tridimensionale: il campo elettromagnetico (Figura 2). Ciò ha consentito di passare da un uso limitato a calamite e cariche elettrostatiche al mondo moderno, i cui progressi tecnologici sono quasi esclusivamente basati sull'eredità lasciataci da Maxwell ed i suoi colleghi.
Generatori di corrente alternata, linee di trasmissione elettrica, trasformatori e motori funzionano, basandosi su queste equazioni, con campi elettrici che variano lentamente nel tempo (ad esempio la corrente di casa è alternata a 50 Hertz, ossia oscilla 50 volte in un secondo).
Figura 3. Schema di un'onda elettromagnetica
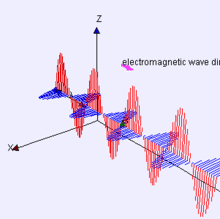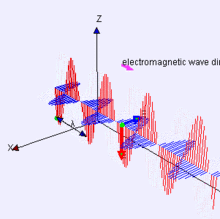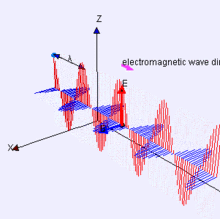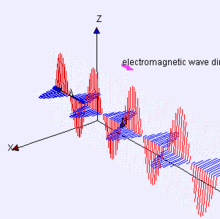
Nel 1865 Maxwell dimostrò, inoltre, che – a partire dalle ”sue” equazioni – era possibile ricavare l’equazione delle onde. Questa equazione si applica a qualunque tipo di fenomeno oscillante ed è quindi la stessa che descrive la propagazione delle onde acustiche, sismiche o marine. Mentre il suono è un’onda di compressione dell’aria lungo la direzione di propagazione, nelle onde elettromagnetiche ad oscillare sono i campi elettrici e magnetici, in un alternarsi periodico e sincrono. Il campo magnetico è sempre ortogonale al campo elettrico ed entrambi sono perpendicolari alla direzione di propagazione dell’onda. Le proprietà sono definite solo dalla lunghezza dell'onda elettromagnetica, ossia la distanza che l’onda percorre – a 300.000 km al secondo – mentre il campo compie una completa oscillazione (Figura 3).
Alternativamente si può usare la frequenza, il numero di oscillazioni al secondo compiute dai campi elettrici e magnetici (la lunghezza d'onda è pari alla velocità della luce diviso la frequenza). Ad esempio, le onde della radio hanno lunghezze d’onda pari a centinaia di metri (o frequenze di MHz) mentre i raggi gamma più intensi possono avere lunghezze d’onda inferiori al nucleo atomico (10-12 m, con frequenze di 1020Hz).
Maxwell e le successive misure sperimentali di Hertz confermarono che la luce visibile altro non era che un’onda elettromagnetica dove, a ciò che noi percepiamo come colori diversi, in realtà corrispondono lunghezze d'onda diverse[2].
Figura 4. La luce solare bianca scomposta da un prisma nei colori fondamentali.
La luce visibile occupa comunque un intervallo ristrettissimo dello spettro delle onde elettromagnetiche (e.m.): tra 0.39 micrometri (rosso) e 0.7 micrometri (blu-violetto) (Figura 4). Il motivo per cui i nostri occhi si sono evoluti per ricevere queste onde non è casuale: è infatti legato al picco delle emissioni della radiazione solare, descritte da un’altra fondamentale equazione della luce, derivata da Planck.
Se l’equazione che descrive la propagazione delle onde e.m. è simile a quella delle onde sonore, marine o sismiche, vi è comunque una fondamentale differenza: un’onda e.m. è in grado di diffondersi liberamente nel vuoto senza la necessità di alcun mezzo che invece – per analogia alle onde meccaniche – si supponeva fosse indispensabile alla sua propagazione. Il problema dell’etere, immaginario supporto per le onde e.m., rimase in sospeso sino all'esperimento di Michelson–Morley del 1887.
La descrizione dell'elettromagnetismo fornita dalle equazioni di Maxwell ha anche il pregio di essere compatibile con la teoria della Relatività speciale[3]. Lorentz derivò infatti le sue trasformazioni di coordinate – alla base della successiva teoria di Einstein – proprio imponendo che dovessero lasciare immutate le equazioni di Maxwell.
Un'altro cruciale lascito delle equazioni di Maxwell è quello dell'unificazione di fenomeni e forze fondamentali della natura, alla base di tutte le ricerche di fisica fondamentale del XX e XXI secolo: la forza elettromagnetica è stata ulteriormente combinata con quella nucleare debole in una teoria ancora più generale. Gli sforzi per associare anche la forza nucleare forte e gravitazionale costituiscono una delle più ambite frontiere della ricerca della fisica moderna.
Note
[1] Il termine magnete deriva dalla città greca (ora presso Smirne, in Turchia) di Magnesia ad Sipylum dove, per la prima volta, fu rinvenuto il minerale di magnetite che esibiva queste proprietà.
[2] L’uso dei prismi aveva già permesso a Newton di mostrare come la luce bianca non fosse altro che la somma di tanti colori diversi. Questi colori furono chiamati fondamentali perché, ad un successivo passaggio nel prisma, non venivano ulteriormente scissi.
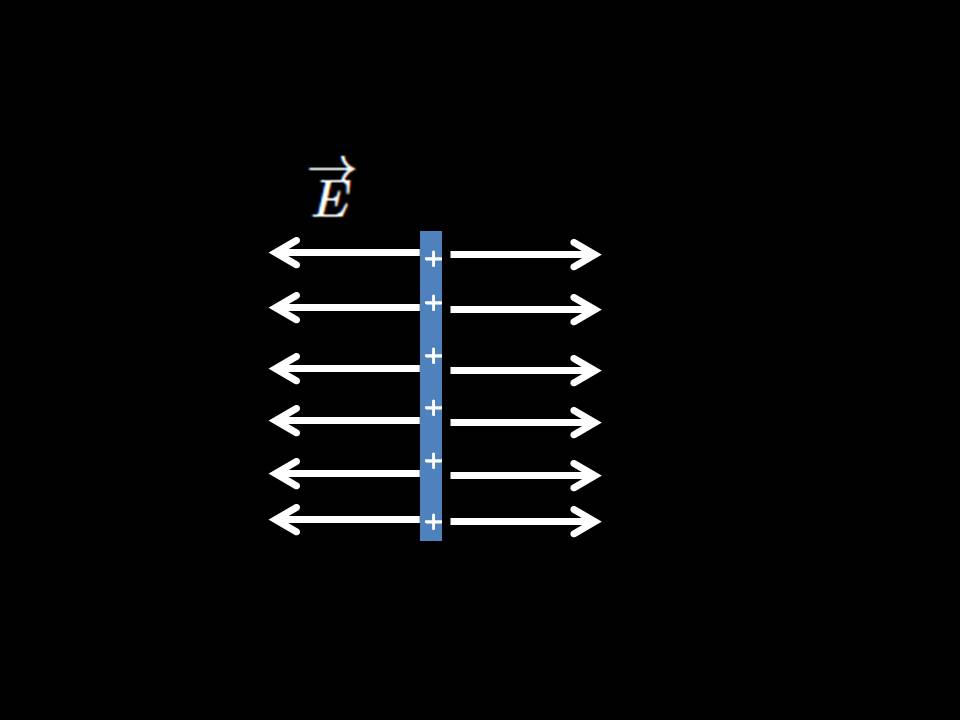
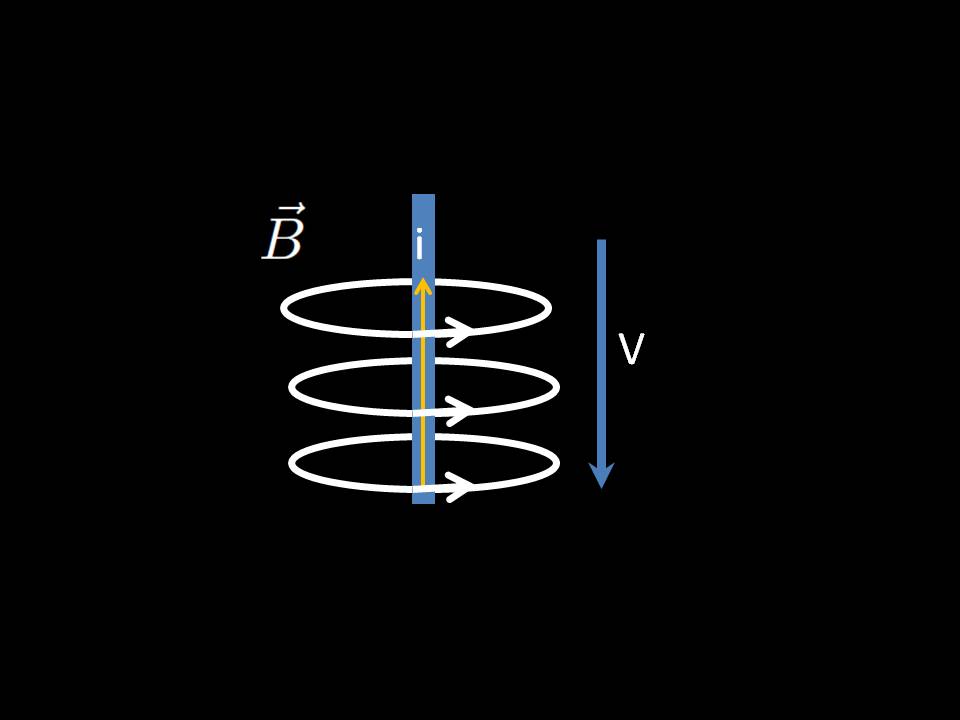
[3] È l'invarianza di questi fenomeni a confermarci che elettricità e magnetismo sono la stessa cosa. Infatti, sappiamo che una carica elettrica stazionaria genera un campo elettrico ed una in movimento genera un campo magnetico. Se quindi prendiamo un filo con una carica elettrostatica percepiamo un campo elettrico. Se invece iniziamo a muoverci rispetto al filo, la carica elettrica sarà in movimento rispetto a noi e misureremo un campo magnetico (Figura 5a e 5b).
Figura 5a. Un filo con una carica elettrostatica genera un campo elettrico con linee di forza radiali
Figura 5b. Se ci muoviamo rispetto al filo non percepiamo più una carica costante ma una corrente e dunque un campo magnetico con linee di forza circolari.
Nessun commento:
Posta un commento